시간복잡도(Time Complexity)
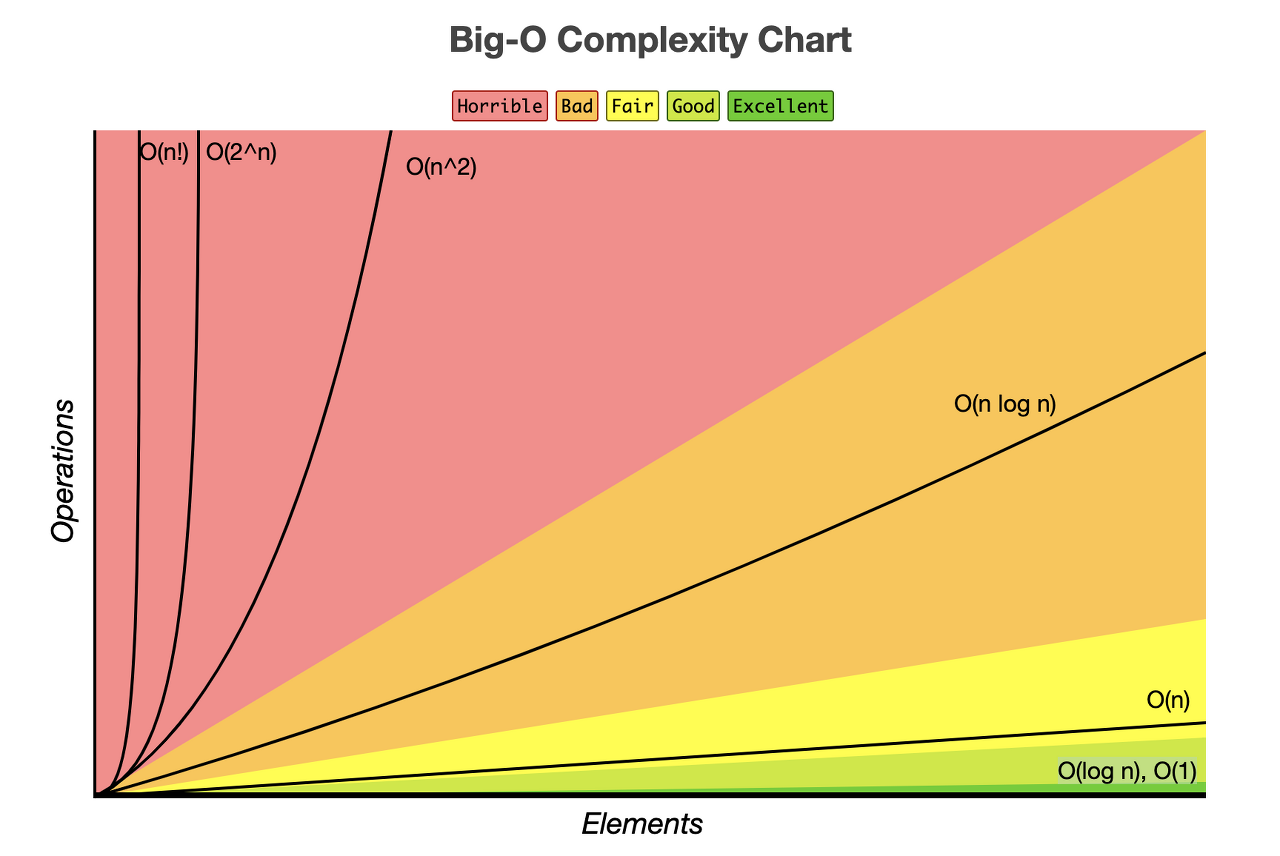
시간복잡도의 예시, 아주 대표적이고 중요한 사진이다. 머릿속에 기억하자
종종 코딩문제를 풀때, for문으로 풀때는 덜한데, while문으로 풀 때 "출력 나오는데 생각보다 오래걸리네" 하는 경험이 있을 것이다.
컴퓨터는 기본적으로 연산하는 놈인데, 연산 횟수가 많으면 자연히 오래걸린다.
우리는 이럴때 자연스럽게 "이거 생각보다 오래걸리는데, 더 빨리하게 못하나?" 하는 생각을 할 때가 많다.
시간 복잡도는 이러한 생각을 수치적으로 나타내는 지표 라고 볼 수 있다.
Big-O 표기법
일단, 위의 그림을 보면 우리가 학창시절에 배웟던 익숙한 그래프가 보인다.
일단 시간 복잡도는 "입력값의 변화에 따라 연산을 실행 했을 때, 연산횟수에 비해 시간이 얼마나 걸리는가"를 수치적으로 나타내는 것이다.
그래서, 코드의 연산방식에 따라 연산할 데이터가 많아지면 기하급수적으로 시간이 늘어나거나, 혹은 처리되는 속도가 일정하거나, 다른 방식에 비해 더 적게 시간이 들어가는 경우도 있다.
그런데 들어가는 데이터에 따라 같은 코드라도 다른 연산시간이 나타날 수 있다. 그래서 Big-O 표기를 한다.
- Big-O : 해당 코드를 실행 했을 때 가장 오래걸리는 경우 (최악)
- Big-Ω : 해당 코드를 실행 했을 때 가장 빨리 결과를 내는 경우 (최선)
- Big-θ : 해당 코드를 실행 했을 때 평균적으로 실행되는 시간 (평균)
우리는 이 코드에 뭐가 들어갈지, 얼마나 들어갈지 모르니 항상 최악을 기준으로 코드를 작성해야 한다.
(업무보고 할때 항상 일정에 마진을 주고 최악의 경우만 따졋을때 기준으로 일정을 조율하는것과 같다. ㅎ)
1. O(1)

시간복잡도 O(1)의 예시 (출처 : 코드스테이츠)
시간복잡도 O(1) 를 가지는 알고리즘은 입력에 따라 항상 균일한 연산속도를 보인다는 특징을 가진다.
입력값이 증가하더라도 출력되는 시간이 늘어나지 않는다. -> 입력값의 크기와 관계 없이 즉시 출력값이 나온다!
O(1) 를 가지는 코드 예시
public int O_1_algorithm(int[] arr, int index) {
return arr[index];
}
int[] arr = new int[]{1,2,3,4,5};
int index = 1;
int results = O_1_algorithm(arr, index);
System.out.println(results); // 2단순히 배열에서 인덱스에 해당하는 출력을 꺼내는 코드이므로, 입력값을 크기와 관계없이 항상 일정한 시간이 걸린다.
2. O(n)

시간복잡도 O(n)의 예시 (출처 : 코드스테이츠)
O(n)은 입력값이 증가하면 출력값도 비례해서 늘어나는 경우다.
만약 1부터 들어온 숫자 N까지 순서대로 출력하는 코드를 작성한다고 하자, 숫자가 하나 나오는데 1초가 걸린다고 치면
N 이 5로 들어오면 -> 5초
N이 10으로 들어오면 -> 10초
....
N이 100으로 들어오면 -> 100초
N의 크기에 비례해서 출력되는 시간이 달라지는 것이다.
코드 예시
public void O_To_N(int n) {
for(int i = 0; i <= n; i++) {
System.out.println(i);
}
}그런데 주의할점은, 이렇게 일차함수 처럼 시간이 늘어나기만 하면 O(n)이라고 한다는 것이다.
public void O_To_N(int n) {
for(int i = 0; i < n * 2; i++) {
System.out.println(i);
}
}위의 코드는 n에 2배씩 늘어나게 된다.
n에 5가 들어가면 -> 10초
n에 10이 들어가면 -> 20초
.....
"앞선 코드보다 2배 늘어나니까 O(2n)이네!" 할 수도 있다.
하지만, 위 코드, 아래 코드 둘 다 입력값이 커질수록 O(n)의 n 앞에 붙는 수의 이미가 없어진다 (n이 계속 커져서 무한대에 가까우면 결국 둘다 무한대니까 라고 슬쩍 넘어가자)
고로, 두 코드 모두 O(n)으로 표기한다.
3. O(log n)

시간복잡도 O(log n)의 예시 (출처 : 코드스테이츠)
O(log n)은 쉽게 말해서 연산을 할 수록 시간이 줄어든다고 보면 된다.
앞서 설명한 O(1)다음으로 빠른 시간복잡도인데, 사실 값을 조회하는것 이외에 뭔가를 계산해서 도출해내야 하는경우 이 시간 복잡도를 목표로 코딩하는것이 가장 바람직하다.
(사실, 잘 안된다 ㅎ)
O(log n)의 경우 가장 적절한 예시가 이진탐색이다.
이진탐색은 왼쪽노드에 부모노드보다 작은 값을, 오른쪽 노드에 부모보다 큰 수를 배치하면서 이진 트리를 만들고, 거기서 답을 찾는 것과 비슷하다.
뭔말이냐고?
그냥 연산할때마다 연산해야 하는 데이터 수가 반으로 줄어든다고 생각하면 된다.
만약 나이 알아맞히기 업 다운 게임을 한다고 하자. (가장 대표적인 예시이다.)
- 1~100 중(사람 나이니까) 임의의 숫자 (나이, 30세로 지정)을 구한다고 하자
- 일단 50업인지 다운인지 물어보면 , 30은 50 보다 작으니, 다운 -> 1~100 에서 1~50으로 범위가 줄어듦
- 1~50으로 줄어들었으니 다시 중간값(25) 업다운을 물어봄 -> 30은 25를 넘으니 업 하면 -> 25~50 으로 범위 줄어듦
- 이처럼 경우의 수를 반으로 줄여가면서.... 최악의 경우 남은 숫자가 2개 남을때 까지 업다운 후 둘중의 하나 고르면 끝
여기서 핵심은 연산을 하는 도중에 연산횟수(연산범위)가 줄어든다는 것이다.
만약 그냥 1~100까지 수 중에 이진탐색을 안하고 1이에요? 2예요? 3이에요? 하나하나 물어보면 나이가 80살이면 80번 물어봐야 할 것이다.(시간복잡도 O(n))
위에서는 반씩 줄여가기 때문에 그보다 훨씩 적은 횟수만 연산해서 원하는 값을 도출 가능하다. (O(log n))
4. O(n^2)

시간복잡도 O(n^2)의 예시 (출처 : 코드스테이츠)
시간복잡도 O(n^2)는 입력값이 증가하면 연산시간이 n의 제곱수의 비율로 증하가는 경우다.
만약 1초 걸리던 알고리즘에 5를 넣었는데, 25초 (입력값 5^2초)가 걸린다면 O(n^2)의 시간복잡도를 가지는 알고리즘이라는 것이다.
뭔지 모르겠다고?
가장 대표적인 예시가 이중 for문이다.
코드예시
public void O_quadratic_N(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
System.out.println(i);
}
}
}위의 코드에서 이중 for문으로, 같은 연산이 n*n번 돌게 되어 있다.
(안쪽의 for문이 다 돌면, 바깓의 for문의 i값이 1 올라가고 또 안쪽의 for문을 돌린다. )
이처럼, 입력값(n)이 증가함에 따라 n*n(n^2)형태를 띄는 알고리즘의 시간복잡도를 O(n^2)라고 한다.
그런데, 이중 for문 말고 또 하나 더 넣어서 삼중으로 만들면 O(n^3)이네? 라고 생각 할 수 있다.
코드예시
public void another_O_quadratic_algorithm(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
for(int k = 0; k < n; k++) {
// do something for 1 second
}
}
}
}앞에서 O(n) 시간 복잡도를 내부에 상관 없이 (O(n), O(2n) 상관 없이) 다 O(n)라고 부르는 것 처럼, O(n^3)인 경우도 O(n^2)로 부른다.
"얼마나 시간이 늘어나냐" 가 중요한것이 아니라, "어떤식으로 늘어나느냐(어떤 구조로 늘어나느냐)"가 시간복잡도 분류의 핵심이다.
5. O(2^n)

시간복잡도 O(2^n)의 예시 (출처 : 코드스테이츠)
시간복잡도 O(2^n)은 시간복잡도 중에서 가장 느린 복잡도를 가진다.(연산 시간이 제일 길다.)
데이터가 늘어날수록 연산시간이 기하급수적으로 늘어나는 형태로 마치 발산하는듯한 형태이다.
가장 대표적인 예로 피보나치를 재귀함수로 구현한 예시가 있다.
코드 예시
public int fibonacci(int n) {
if(n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci (n - 2);
}n이 증가하면 작동되는 재귀함수는 기하급수적으로 늘어난다.
n이 40이여도 수 초가 걸리고 100이면 평생 결과를 반환받지 못할 수도 있다고 한다.
코딩테스트에서 시간복잡도를 정하는 팁
입력으로 주어지는 데이터 크기를 잘 보면 된다.
만약 통상적인 100~1000 정도의 혹은 그보다 조금 더 입력 데이터가 들어온다면 O(n)으로 시간복잡도를 설정하고 그에 맞게 코딩을 진행하면된다.
하지만 100000000처럼 엄청 큰 데이터는 분명 시간복잡도O(n)으로 하면 채점 기준 중 일정 시간 오버가 되어 틀렷다고 나올 것이다.
여기서 우리는 O(log n)시간복잡도를 목표로 코드를 작성하여 해결해야 한다는것을 알아채야 한다.
핵심은 "주어진 데이터 수에 따라 목표로 하는 시간복잡도를 달리해야 한다."
데이터가 고만고만, 혹은 작으면 : O(n)
데이터가 무진장 크면 : O(log n)
'백엔드 > JAVA_이론공부' 카테고리의 다른 글
| JAVA_자료구조_해시 맵 (hash map) (2) | 2023.02.18 |
|---|---|
| JAVA_자료구조_(Binary Search Tree, 트리 순회) (0) | 2022.11.28 |
| JAVA_자료구조_(Graph) (0) | 2022.11.28 |
| JAVA_자료구조_트리(Tree) (0) | 2022.11.28 |
| JAVA_자료구조_큐(Queue) (1) | 2022.11.28 |